Kunci Jawaban
Kunci Jawaban Matematika Kelas 8 Halaman 183-184 Kurikulum Merdeka : Menentukan Peluang Kejadian
Kunci jawaban pelajaran Matematika kelas 8 SMP/MTs halaman 183-184 Kurikulum Merdeka. Soal yang diberikan berisi menentukan peluang kejadian.
Penulis: Content Writer Tribun Solo | Editor: Hanang Yuwono
TRIBUNSOLO.COM - Berikut kunci jawaban pelajaran Matematika kelas 8 SMP/MTs halaman 183-184 Kurikulum Merdeka.
Pada buku Matematika kelas 8 Halaman 183-184 terdapat 4 soal yang harus dijawab oleh siswa, dimulai dari soal nomor 4.
Soal yang diberikan berisi menentukan peluang kejadian.
Baca juga: Kunci Jawaban Tema 2 Kelas 3 Halaman 184-185 : Menyayangi Hewan dan Tumbuhan
Kunci jawaban ini diguanakan sebagai panduan orangtua dalam mengoreksi pekerjaan anak.
Diharapkan siswa mengerjakan soal yang telah diberikan secara mandiri sebelum melihat kunci jawaban.
Berikut kunci jawaban Matematika kelas 8 halaman 183-184
Beragam Peluang
Soal 4
Baca juga: Kunci Jawaban Ekonomi Kelas 11 Halaman 57 Kurikulum Merdeka : Menghitung Pendapatan Nasional
Dua dadu berbeda ukuran dilempar bersamaan. Jawablah pertanyaan-pertanyaan berikut.
(1) Tentukan peluang kejadian jumlah dua mata dadu 4.
(2) Tentukan peluang kejadian jumlah dua mata dadu paling sedikit 10.
(2) Peluang kejadian jumlah dua mata dadu manakah yang terbesar?
Jawaban:
Merdeka kelas 8 halaman 184 soal 6.
(1) Jika jumlah angka mata dadu adalah 4, maka ada 3 cara (1, 3), (2, 2), dan (3, 1), sehingga peluang yang ditemukan adalah 3/36 = 1/12.
(2) Jika jumlah angka mata dadu 10 atau lebih, maka ada 6 cara (4, 6), (5, 5), (5, 6), (6, 4), (6,5), (6, 6), sehingga peluang yang ditemukan adalah 6/36 = 1/6
(3) Jumlah angka mata dadu adalah 7. (Peluangnya adalah 6/36 = 1/6)
Soal 5
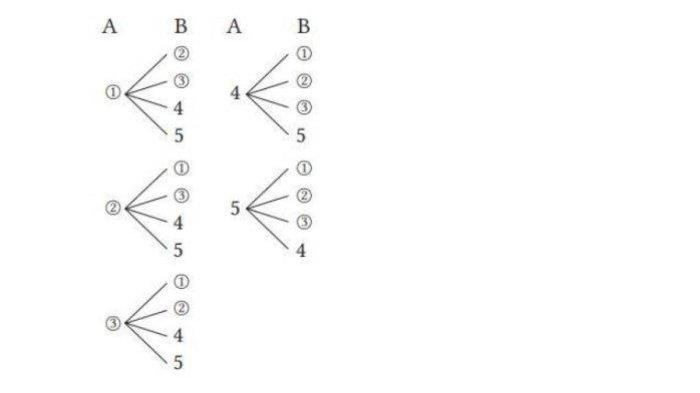
Pada Contoh 2, tentukan peluang bahwa B akan memperoleh tiket berhadiah.
Bandingkan hasilnya dengan peluang A memperoleh tiket berhadiah.
Tentukan pula peluang kedua orang tersebut memperoleh tiket berhadiah.
Jawaban:
Karena kejadian B memperoleh tiket berhadiah ada 8 cara, yaitu (1, 2), (2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (5, 1), dan (5, 2) maka peluang yang kita temukan adalah 8/20 = 2/5.
Dengan demikian, perbandingan peluang A dan B adalah sama besar.
Selain itu, karena kejadian A dan B memperoleh tiket berhadiah ada 2 cara, maka peluang yang kita temukan adalah 2/20 = 1/10.
Soal 6
Pada Contoh 2, bila ada 3 tiket berhadiah dan 2 tiket tidak berhadiah, tentukanlah peluang bahwa A akan memperoleh tiket berhadiah dan peluang B memperoleh tiket berhadiah.
Jawaban:
Jika 1, 2, 3 yang meleset kita jadikan 4, 5, maka

Peluang A memperoleh tiket berhadiah adalah 12/10 = 3/5
Peluang B memperoleh tiket berhadiah adalah 12/20 = 3/5
Soal 7
Ada tiga kartu dan salah satu kartu tersebut merupakan tiket berhadiah.
Bila ada tiga orang mengambil tiga kartu tersebut dalam urutan tertentu tanpa pengembalian, apakah peluang memperoleh kartu berhadiah bergantung pada urutan pengambilan?
Jelaskan jawabanmu berdasarkan gagasan peluang.
Jawaban:
Jika yang cocok 1, yang meleset menjadi 2, 3

Peluang: Pengertian dan Rumusnya
Dalam kehidupan sehari-hari kerap terdengar istilah peluang. Apa yang dimaksud dengan peluang, terutama dalam ilmu matematika dan bagaimana rumus peluang? Berikut adalah pembahasannya!
Pengertian peluang
Ada berbagai peristiwa ataupun kejadian yang terjadi dalam kehidupan sehari-hari. Dilansir dari Khan Academy, setiap kali kita tidak yakin tentang suatu peristiwa kita dapat memperkirakan seberapa besar kemungkinan peristiwa tersebut terjadi.
Dalam matematika, kemungkinan tersebut disebut sebagai peluang atau probabilitas. Sederhananya peluang adalah seberapa besar kemungkinan sesuatu akan terjadi.
Dilansir dari Cuemath, nilai peluang untuk suatu kejadian atau peristiwa berada antara 0 dan 1.
Di mana jika peluang sama dengan nol, maka kejadian tersebut tidak akan terjadi. Sebaliknya, jika peluang sama dengan 1 maka kejadian tersebut pasti akan terjadi.
Rumus peluang
Baca juga: Kunci Jawaban Bahasa Indonesia Kelas 7 Halaman 37 Kurikulum Merdeka: Bab 2, Pertanyaan Pemantik
Peluang dapat dihitung dari rasio banyaknya suatu anggota kejadian dibagi dengan jumlah kejadian. Sehingga, rumus peluang dapat dituliskan sebagai berikut!

Dengan,
P(A): peluang suatu kejadian
n(A): banyaknya anggota kejadian
n(S): Banyaknya seluruh kejadian atau ruang sampel
Makin besar nilai n(A), maka akan makin besar peluang suatu kejadian untuk muncul. Sedangkan, makin kecil nilai n(A), maka akan makin kecil juga peluang suatu kejadian akan muncul.
Contoh peluang
Misalnya, suatu koin memiliki dua sisi. Satu sisinya adalah gambar, sedangkan sisi lainnya adalah angka.
Ketika kita melempar koin tersebut, hanya ada dua kemungkinan sisi koin yang berada di atas (gambar atau angka).
Artinya, peluang munculnya sisi koin angka dan gambar adalah sama-sama 50 persen atau 0,5.
Adapun, peluang terlihat saat kita mengocok dadu. Dadu akan menunjukkan salah satu dari keenam sisinya. Peluang munculnya sisi dadu dengan angka 1 adalah 1 dari 6 kejadian atau 1,66.
*) Disclaimer:- Jawaban di atas hanya digunakan untuk memandu proses belajar siswa.
(Magang TribunSolo.com/Siti Mariam Ayuni)
| Kunci Jawaban Tema 2 Kelas 3 Halaman 184-185 : Menyayangi Hewan dan Tumbuhan |

|
|---|
| Kunci Jawaban Bahasa Jawa Kelas 9 Halaman 32 : Unsur Intrinsik Teks Andhe Andhe Lumut |
|
|---|
| 20 Latihan SBdP Kelas 3 Semester 1 Kurikulum Merdeka, Lengkap Disertai Kunci Jawaban |

|
|---|
| Kunci Jawaban Tematik Tema 3 Kelas 6 Halaman 63 : Penemuan dan Manfaatnya |

|
|---|
| Kunci Jawaban PKN Kelas 8 Halaman 67 Kurikulum Merdeka: Tata Negara dan Pemerintahan |
|
|---|

















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.